백준 2263번
문제
n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복 없이 매겨져 있다. 이와 같은 이진 트리의 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 n(1≤n≤100,000)이 주어진다. 다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고, 그 다음 줄에는 같은 식으로 포스트오더가 주어진다.
출력
첫째 줄에 프리오더를 출력한다.
트리의 중위 순회(Inorder), 후위 순회(Postorder) 탐색 결과가 주어졌을 때 전위 순회 탐색 결과를 출력하는 문제!
접근 과정
처음에는 중위 순회로 만들 수 있는 트리 중 후위 순회를 만족하는 트리를 구성하는 방법을 고민했다. 하지만 노드의 최대값이 크기 때문에 가능한 경우의 수가 너무 많고 하나의 순회로 트리를 구성하는 규칙을 일반화하기도 어려웠다.
지하철에서 수첩에 트리를 그려가며 고민하다보니 다음과 같은 규칙을 발견할 수 있었다.
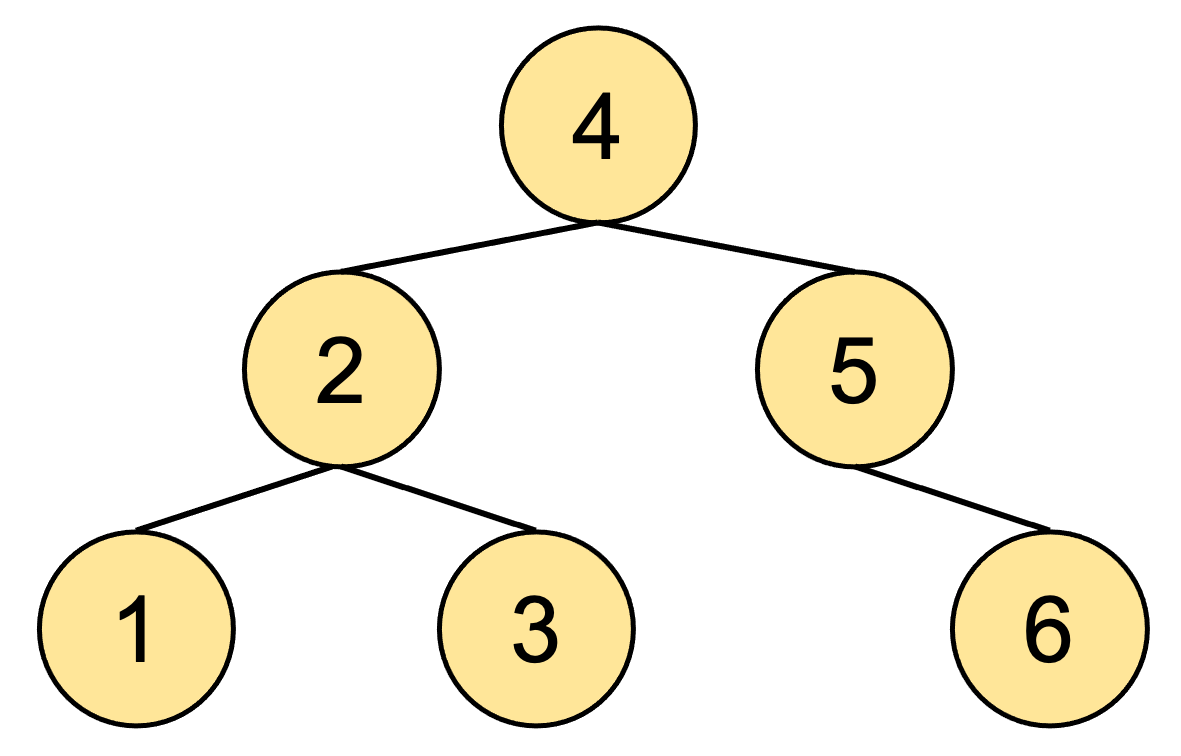
중위 순회: 1 - 2 - 3 - 4 - 5 - 6
후위 순회: 1 - 3 - 2 - 6 - 5 - 4
우선 후위 순회의 맨 마지막 방문 노드는 반드시 루트 노드이다. 또한 중위 순회에서 루트 노드를 방문한 시점을 기준으로 왼쪽은 모두 루트 노드의 왼쪽 자식에 포함되는 집합이며 오른쪽도 모두 루트 노드의 오른쪽 자식에 포함되는 집합이다.
중위 순회(왼 쪽): 1 - 2 - 3
루트노드: 4
중위 순회(오른쪽): 5 - 6
이를 통해 루트 노드의 왼쪽에 위치한 수와 오른쪽에 위치한 수(배열의 길이)를 구할 수 있으며 후위 순회에서 루트 노드를 제외하고 각 길이만큼 나누게되면 각 자식 노드에 대해 후위 순회를 수행한 결과가 된다.
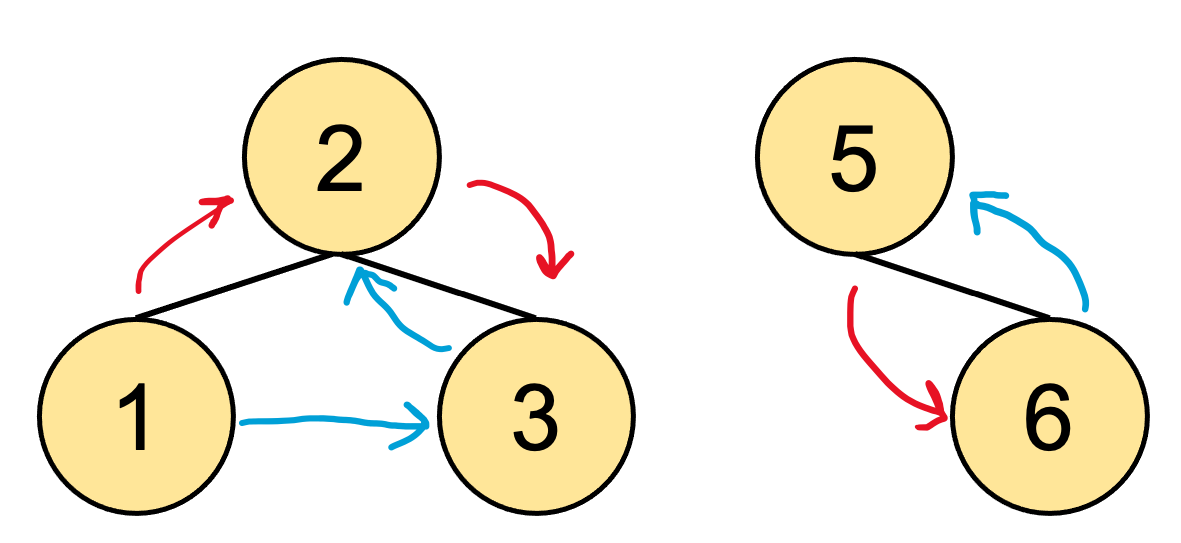
중위 순회(왼 쪽): 1 - 2 - 3
후위 순회(왼 쪽): 1 - 3 - 2
중위 순회(오른쪽): 5 - 6
후위 순회(오른쪽): 6 - 5
이를 통해 루트 노드를 왼쪽/오른쪽 자식이 루트 노드가 되는 트리의 전위 순회와 후위 순회 결과를 얻을 수 있게된다. 그렇다면 첫 입력 값에서 길이만 짧아진 셈이니 각 트리에 대해서 동일한 알고리즘을 적용할 수 있을 것이다.
후위 순회를 통해 찾은 루트 노드로 반절씩 트리를 분할하다보면 새로운 트리를 만들 수 있을 뿐만 아니라 분할 후 탐색 과정을 루트 -> 왼쪽 -> 오른쪽과 같이 구현하면 단번에 전위 수행 결과를 얻을 수도 있다.
결과적으로 이 문제는 분할 정복 알고리즘을 통해 해결할 수 있는 문제이고 그 순서를 정리하면 아래와 같다.
1. 후위 순회 결과 맨 끝에서 루트 노드를 확인한다.
2. 중위 순회 결과에서 루트 노드를 찾는다.
3. 루트 노드를 찾은 위치를 기준으로 왼쪽에 위치한 노드의 수와 오른쪽에 위치한 노드의 수를 구한다.
4. 왼쪽에 위치한 노드들에 대하여 1번의 과정을 반복한다.
5. 오른쪽에 위치한 노드들에 대하여 1번의 과정을 반복한다.
이를 재귀호출을 통해 구현하여 통과 할 수 있었다. 다만 실행시간이 꽤 늘어졌는데 이는 위 알고리즘의 2번 루트 노드를 찾는 과정을 다음과 같이 구현했기 때문이었다.
int rootIndex;
for (rootIndex = inBegin; rootIndex < inEnd; +rootIndex) {
if (inorder[rootIndex] == root) { break; }
}
중위 순회 결과를 하나하나 탐색하며 루트 노드를 찾는데 트리의 모양에 따라 즉시 찾을수도 모든 노드를 탐색해야 찾을 수도 있다. \(O(N\log N)\)의 시간 복잡도가 최악의 경우에는 \(O(N^{2})\)이 될 수 있는 것이다. 다행히 중위 순회 결과에서 루트 노드의 위치를 찾는 연산을 \(O(1)\)의 시간으로 해결하는 방법이 있었고 이를 통해 실행 시간이 획기적으로(1148ms -> 28ms) 줄어들게 되었다. 다른 사람의 코드를 살펴보니 실행시간이 빠른 사람들은 대부분 똑같은 방법으로 구현하고 있던데 직접 설명하는 것보다 코드를 보며 확인해보면 좋을 것 같다.
소스 코드
#include <iostream>
using namespace std;
int* inorder;
int* postorder;
void makeTree(int inBegin, int inEnd, int postBegin, int postEnd) {
int len = inEnd - inBegin;
if (len <= 0) { return; }
int root = postorder[postEnd - 1];
cout << root << ' ';
// 시간복잡도 O(1)으로 루트 노드의 위치를 얻는다.
int rootIndex = inorder[root];
// make left
int rightLen = inEnd - rootIndex - 1;
makeTree(inBegin, rootIndex, postBegin, postEnd - rightLen - 1);
// make right
makeTree(rootIndex + 1, inEnd, postEnd - rightLen, postEnd - 1);
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(nullptr);
int n, tmp;
cin >> n;
inorder = new int[n + 1];
postorder = new int[n];
for (int i = 0; i < n; ++i) {
// 분할의 기준이 되는 루트 노드는 후위 순회
// 결과에서 얻을 수 있으므로 중위 순회 결과의
// 순서를 유지할 필요가 없다. 위치만을 저장한다!
cin >> tmp;
inorder[tmp] = i;
}
for (int i = 0; i < n; ++i) {
cin >> postorder[i];
}
makeTree(0, n, 0, n);
delete inorder;
delete postorder;
return 0;
}